| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 알고리즘
- 카카오 서류전형
- 2629
- 백준12738
- 1670
- 카카오 인턴십
- 기술면접
- 백준
- 백준12015
- Python
- 여름인턴십
- 카카오 자기소개서
- DP
- 개발자 면접
- 정상회담2
- 단어수학
- 카카오 면접
- 카카오
- 파이썬
- 2482
- 인턴십 면접
- 구간나누기
- 가장긴증가하는 부분수열
- LIS 알고리즘
- 2228
- LIS
- 백준11053
- 최장증가수열
- Longest Increasing Subsequence
- 카카오 인턴
- Today
- Total
프로그래밍에 대한 고찰 및 생각
[4][그래프 이론] - 위상정렬 (Topological Sorting) 본문
올해로 20살이된 민수는 코로나 여파로 겨울방학임에도 불구하고 집에서 나갈 수 없어 옛 추억을 떠올리며 오랜만에 스타크래프트 게임을 시작했다.
평소에 프로토스 종족을 좋아하던 민수는 부푼마음으로 게임을 시작했지만 너무 오랜만에 하는 탓에 지어야 할 건물들의 순서를 몰라 난관에 부딪혔다.

스타크래프트 라는 게임에서는 각 종족마다 많은 건물들이 존재한다.
그러나 이러한 건물들을 게임을 처음 시작하면 바로 건설할수 없는 건물들이 있으며 이 건물들은 지정된 다른 건물들을 먼저 선행으로 건설해야 건설할 수 있다.
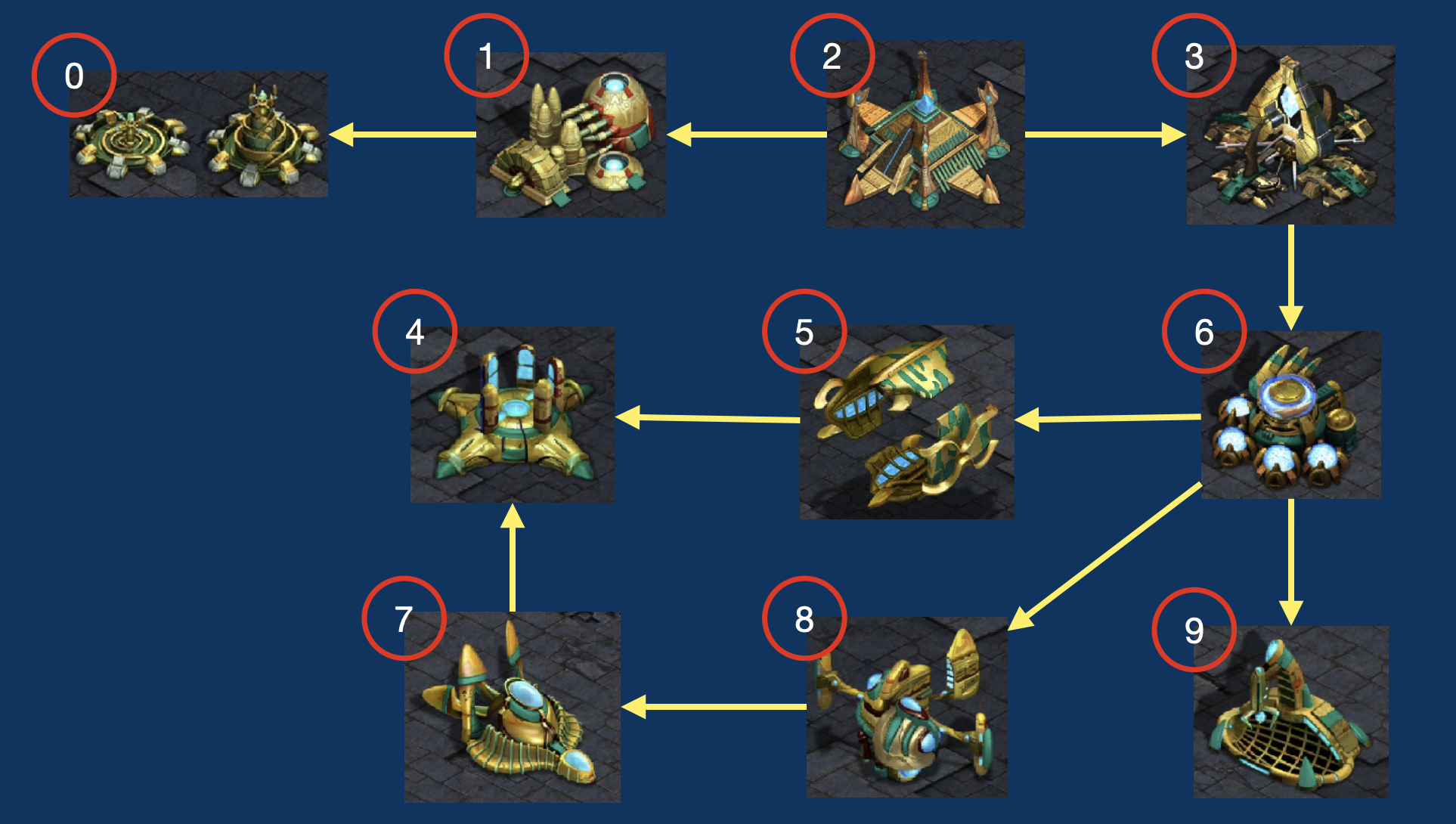
예를 들어 0번 건물을 짓기위해서는 1번건물을 지어야한다.
그런데 1번 건물을 지으려면 2번 건물을 지어야한다.
즉 2->1->0 의 순서로 건물을 지을 수 있다.
위와같은 건물의 순서도를 참고해서 10개의 건물을 모두 지을수 있게 민수에게 지어야 할 건물의 순서를 알려주도록 해보자.
위상정렬 (Topological Sorting) 이란?
위상정렬이라함은 방향이 있는 그래프에서 각 정점들의 방향을 거스르지 않게 나열하는 것을 의미한다.
앞선 예시처럼 의존성이 존재하는 건물들의 건설 순서를 구하는것도 결국 위상정렬의 하나의 예시로 볼 수 있다.
위상정렬 조건
위상정렬은 각 정점들의 방향을 거스르지 않게 나열해야하므로 그래프내에서 순환이 존재해서는 안된다.
만약
1. 밥을 먹기위해서는 돈이 필요하고,
2. 돈을 벌기위해서는 일을 해야하고,
3. 일을 하기 위해서는 밥을 먹어야한다고 하자.
이런 경우 3가지일을 순서가 위배되지 않게 정렬할수 없다.
만약 밥을 먹저 먹는다고 하면 밥을 먹었으니 일을 할수 있게되고, 일을 하면 돈을 벌수 있다.
하지만 애초에 밥을 먹으려면 돈이 있어야 하므로 뫼비우스의 띠처럼 끝없이 사전조건을 만족시키지 못하게 된다.
위상정렬 설계
위상정렬은 깊이 우선 탐색(DFS)을 이용하여 설계할 수 있다.
DFS를 통해 모든 정점을 방문하면서 더이상 방문할 정점이 없을때 스택에 해당 정점을 추가하는 과정을 반복하고
모든 정점을 순회한 뒤에 스택을 반대로 뒤집으면 위상정렬의 결과가 나온다.
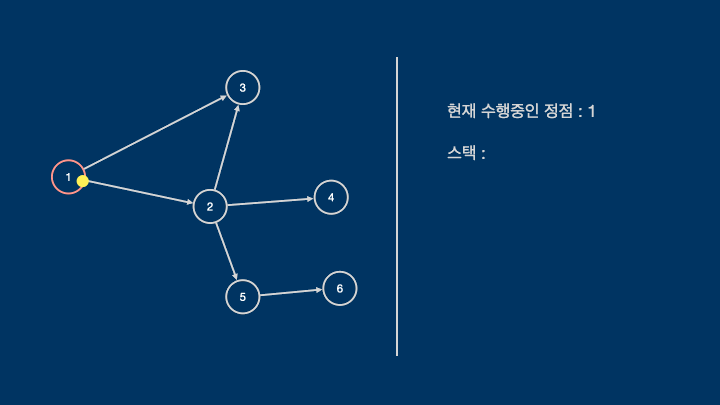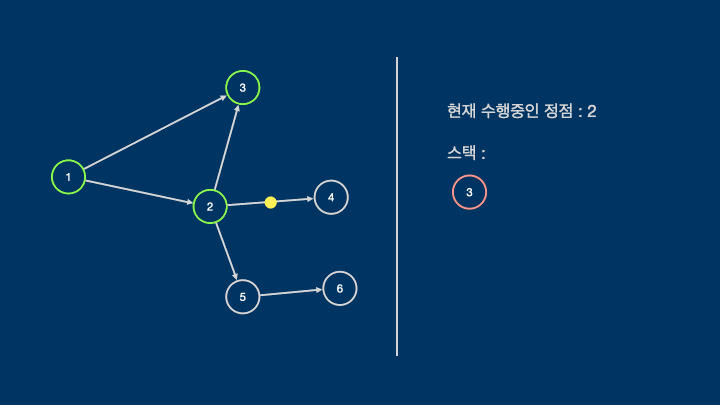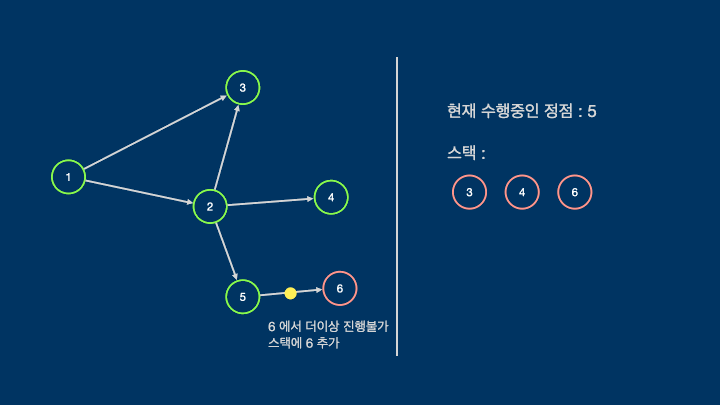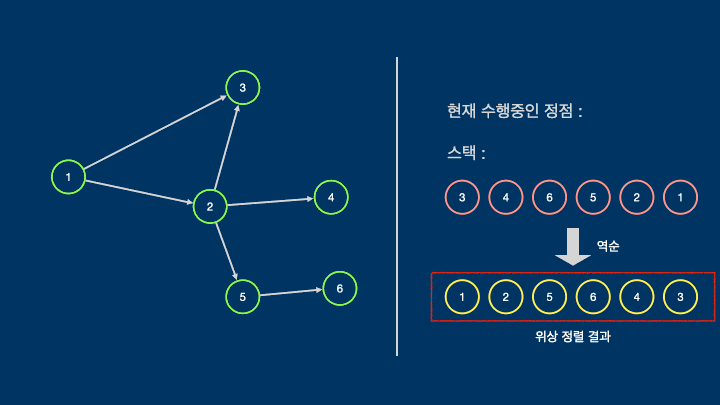
다음은 위의 스타크래프트 건물의 예시를 c++로 작성한 위상정렬 코드이다.
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
vector<vector<int> > graph;
stack<int> s;
int visited[10]; // 0 - 미방문 / 1 - 방문
void dfs_togological(int v){
visited[v] = 1;
for(int i=0; i<graph[v].size(); i++){
if(visited[graph[v][i]] == 0){
dfs_togological(graph[v][i]);
}
}
s.push(v);
}
void dfs_all_topological(){
for(int i=0;i<graph.size();i++){
if(visited[i] == 0){
dfs_togological(i);
}
}
}
void print_topological_sort(){
int tmp;
while(s.size() > 0){
tmp = s.top();
s.pop();
cout << tmp << " ";
}
}
int main(){
for(int i=0;i<10;i++){
graph.push_back(vector<int>());
visited[i] = 0;
}
graph[1].push_back(0);
graph[2].push_back(1);
graph[2].push_back(3);
graph[3].push_back(6);
graph[6].push_back(5);
graph[6].push_back(8);
graph[6].push_back(9);
graph[5].push_back(4);
graph[8].push_back(7);
graph[7].push_back(4);
dfs_all_topological();
print_topological_sort();
}
정렬 결과

결과적으로 아래와같은 위상정렬 결과를 얻게되고 아래와같은 순서로 건물을 짓는다면 문제없이 모든 10개의 건물을 건설 할 수 있을 것이다.

'알고리즘 > 그래프 이론' 카테고리의 다른 글
| [5][그래프 이론] - 오일러 서킷, 한붓그리기 (Eulerian Circuit) (0) | 2021.02.11 |
|---|---|
| [3][그래프 이론] - 너비 우선 탐색 BFS (Breadth-First Search) (0) | 2021.01.27 |
| [2][그래프 이론] - 깊이 우선 탐색 DFS (Depth-First Search) (0) | 2021.01.27 |
| [1][그래프 이론] - 그래프 표현 및 정의 (0) | 2021.01.26 |




