| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 1670
- 파이썬
- Python
- 카카오 인턴십
- 알고리즘
- 카카오 면접
- 2629
- 백준12015
- 2228
- 기술면접
- DP
- Longest Increasing Subsequence
- LIS
- 가장긴증가하는 부분수열
- 단어수학
- 카카오
- 백준12738
- 카카오 자기소개서
- 정상회담2
- 개발자 면접
- 인턴십 면접
- 카카오 인턴
- 여름인턴십
- 백준11053
- 최장증가수열
- 카카오 서류전형
- 백준
- 2482
- LIS 알고리즘
- 구간나누기
- Today
- Total
프로그래밍에 대한 고찰 및 생각
[알고리즘][13][백준_2618][c++] - 경찰차 본문


1. 문제 이해
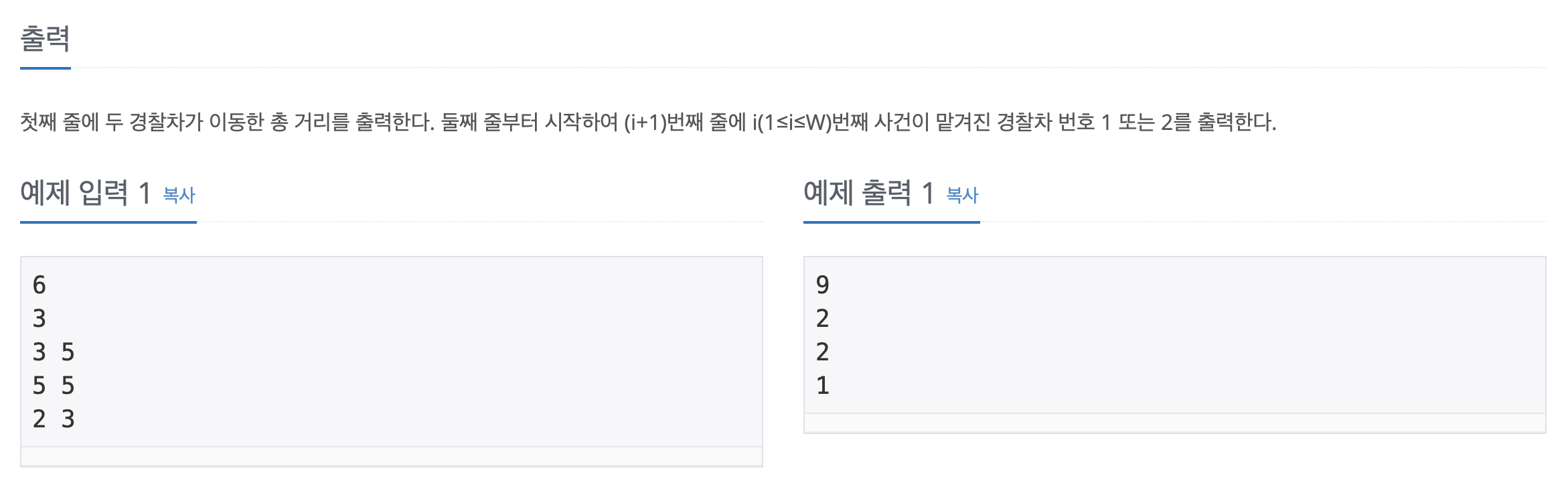
경찰차 문제는 (1,1), (n,n) 에 위치한 경찰차 두대가 w개의 사건들을 가장 짧은 거리를 이동하여 처리하는 문제이다.
주의해야할 부분은 한 경찰차가 하나의 사건을 처리한후 다시 원래자리로 돌아가는 것이 아니라 그 자리에서 다음사건을 처리하게 되고,
사건들은 같은 장소에서 여러번 일어날 수 있다는 점이다.
2. 알고리즘 전략

먼저 문제의 예시를 통해 시나리오를 분석해보자.
경찰차는 (1,1) 그리고 (6,6)에 위치해있고 3개의 사건이 분포되어있다.
만약 첫번째 사건을 처리한다고 가정해보자.
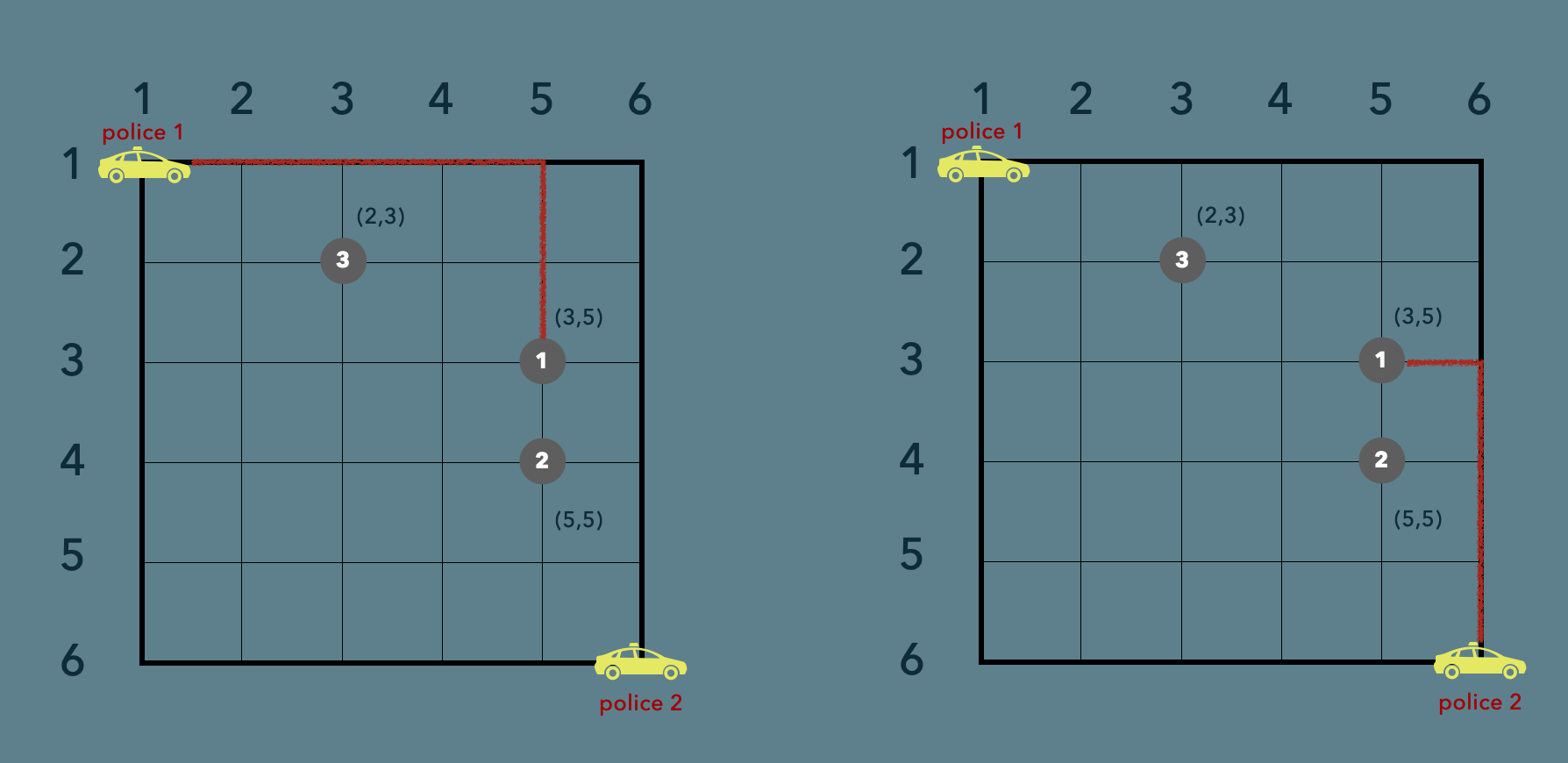
위와같이 1번 경찰차가 6칸을 이동하여 1번 사건을 처리할수도 있고,
2번 경찰차가 4칸을 이동하여 1번 사건을 처리할수도 있다.
그렇다면 총 몇번 시도를 해봐야 모든 경우의 수를 다 탐색해 볼 수 있을까.
각 사건마다 두개의 경찰차중 하나가 사건을 처리할수 있으므로
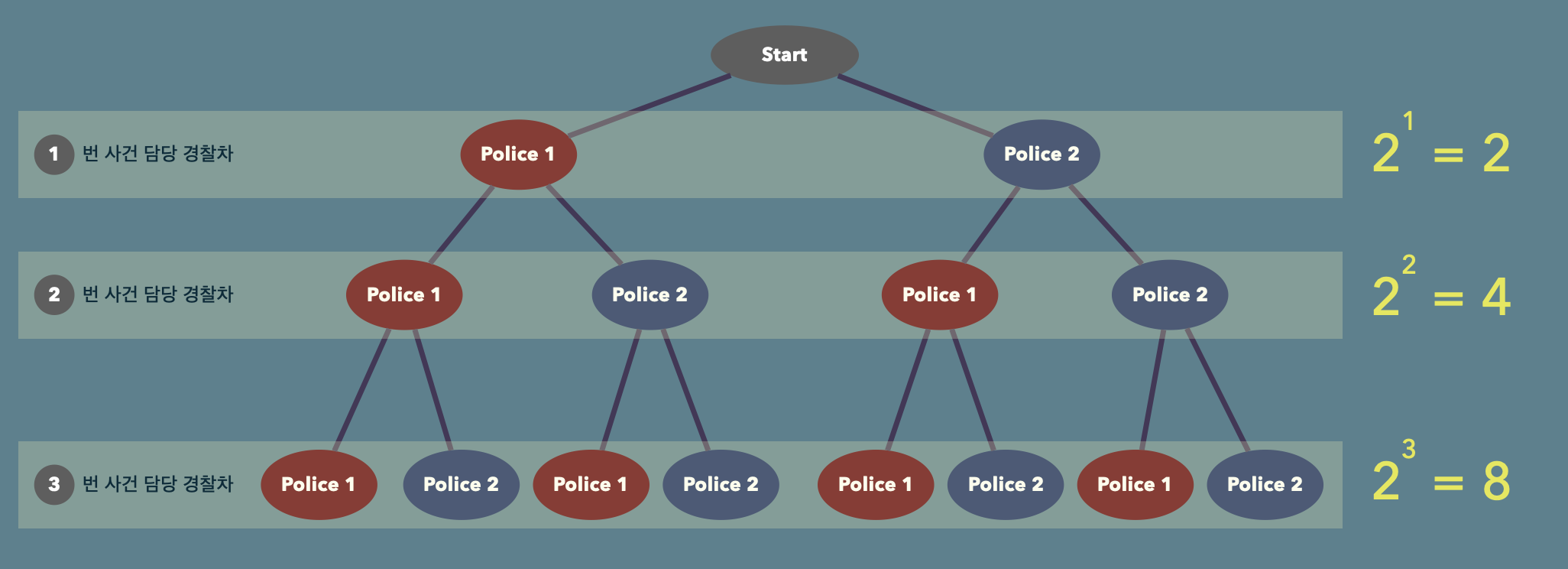
위와같이 한 사건마다 2개의 가지로 분리될것이다.
따라서 w개의 사건이 있다면 총 2^w 개 만큼의 경우의 수가 생긴다.
문제에서 w의 범위가 1 <= w <= 1000 이므로 만약 w = 1000일때
최대 2^1000 가지의 경우의 수가 발생하므로 모든 경우를 brute-force로 해보는것은 불가능하다.
이 문제에서 DP를 적용할 수 있는 부분은 어디일까?
위 문제를 조금 간소화 시켜보자.

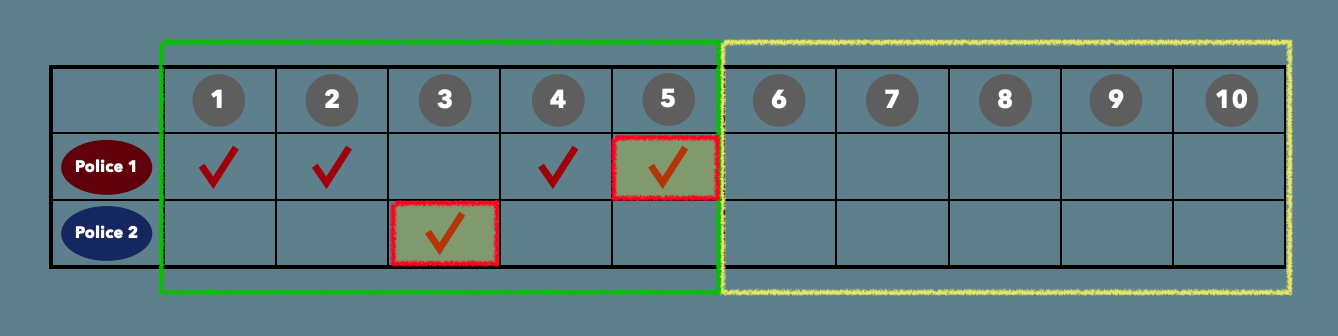
위는 10개의 사건을 처리할수 있는 경우의 수 중 하나를 나타낸 표이다.
간단히 설명하자면 1번 사건은 1번경찰차가 처리하였고,
2번 사건 역시 1번 경찰차가 처리하였다.
그리고 3번 사건은 2번 경찰차가 처리하였고...
이런식으로 진행되는 경우의 수 이다.
그렇다면 여기서 만약 5번 사건까지 파악을 했다고 하자.

그렇다면 6~10번까지의 사건이 아직 배정되지 않은 상황이다.
그리고 경찰차가 배정된 사건묶음을 초록박스로, 배정되지 않은 묶음을 노란 박스로 표시하였다.

이렇게되면 초록박스의 경우의 수는 2^5 개가 되며, 노란박스의 경우의 수도 역시 2^5이 된다.
따라서 총 경우의수는 2^5 * 2^5 = 2^10 임을 알수있다.
이 경찰차 문제에서 가장 중요한 포인트중 하나는 현재 진행 상태를 각 경찰차들의 마지막으로 맡은 사건으로 표현할 수 있다는 점이다.
위와같은 경우 1,2,4,5 번사건을 1번 경찰차가, 3번 사건을 2번 경찰차가 담당하였다.
이는 아래의 4가지 경우와 모두 동일하다.
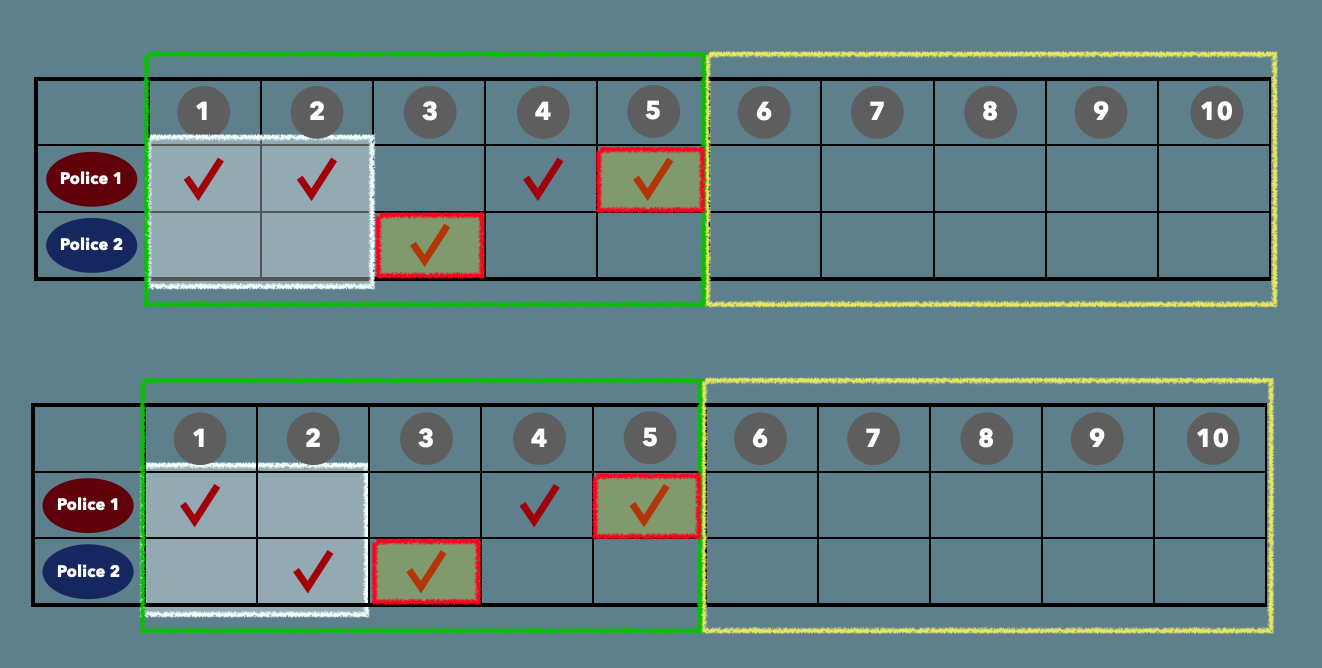

즉 위 4가지 경우에 있어서 이후 6~10까지의 결과값은 모두 동일 할 것이므로 4번 모두 시행해 볼 필요가 없다.
왜 이것이 가능할까?
6번 사건에서 거리의 합에 영향을 받는 부분은 현재 경찰차1,2의 위치이다. 즉 그 위치는 각 경찰차가 마지막으로 맡은 사건의 위치이며 그 위치 이전에 어느 곳을 방문했는지는 이후의 사건에 영향을 주지 못한다.
따라서 2차원배열로 각 경찰차들의 최종 사건을 파라미터로 최소값을 저장하여 DFS에서 DP를 설계할 수 있을것이다.
이렇게되면 경찰차가 이동한 총거리의 최솟값은 구할수있다.
문제는 경찰차가 이동한 총거리 외에 경찰차들이 맡았던 사건들을 나열해야 한다는 것이다.
만약 위의 DP를 활용하여 최솟값과 해당 사건 처리 결과를 string이나 다른 형태로 저장한다고 해도
w^3 = 1000^3 바이트만큼의 메모리를 요구하며 128mb인 문제의 메모리 조건을 뛰어넘게 될것이다.
그래서 생각해 낸 방법은 모든 결과를 항상 누적해서 저장하지 않고 현재 경찰차들의 마지막 사건번호 x,y 를 통해 해당 x,y일때 이후에 최소거리를 만들수 있는 경찰차를 기록해 두는 것이다.
예를 들어 다음과 같은 상황을 가정해보자.
사건은 총 4개이며 현재까지 1번 사건을 1번 경찰차가, 2번 사건을 2번 경찰차가 수행했다고 가정할때, 이후 2번 경찰차가 3번 사건을 담당하는 것이 최소거리를 만든다고 하면 (1,2) 지점의 값은 2가 된다. # 배열에서 인덱싱은 0번부터지만 그림상 1번부터 하도록 하자
해당 지점에는 다음 사건을 담당해야 할 경찰차의 번호가 들어가야한다.

그리고 3번 사건을 2번경찰차가 담당한 후 4번째 사건을 담당해야 할 경찰차의 번호가 (1,3) 지점에 들어가야한다.
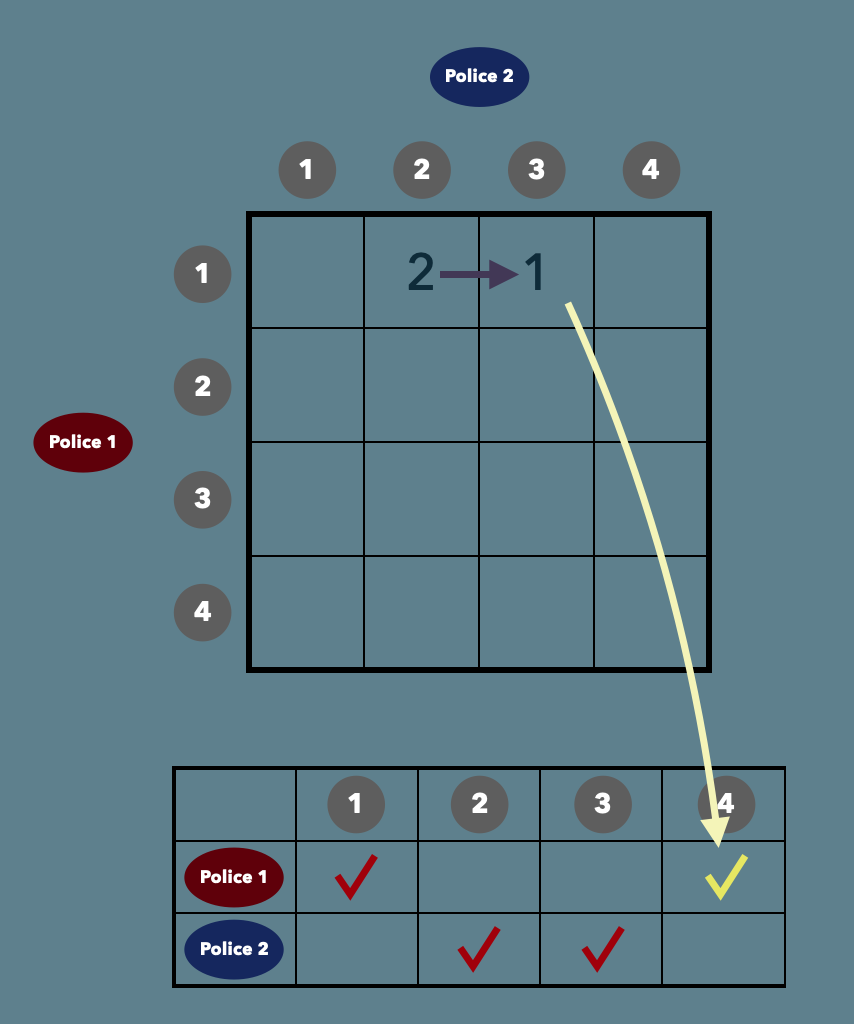
이같은 방법으로 DFS를 통해 뿌리까지 탐색하는 동안 minimum 값이 도출될때마다 현재 경찰차들의 마지막 담당 사건 번호 2가지로 이후 다음사건을 담당해야할 경찰차의 번호를 넣음으로써 최종적으로 모든 사건의 담당 경찰차 순서를 구할 수 있을것이다.
#include <iostream>
#include <utility>
#include <vector>
#include <algorithm>
using namespace std;
int n,w;
vector<pair<int,int> > p;
int store[1010][1010];
int police_store[1010][1010];
// 0 방문전
int calculate_distance(int police, int target, int start){
// start :
// 0 : 두 경찰차 모두 1개이상의 사건을 담당하였다.
// 1 : police가 1,1에 있다.
// 2 : police가 n,n에 있다.
int police_x,police_y,target_x,target_y;
if(start == 1){
police_x = 1;
police_y = 1;
}
else if(start == 2){
police_x = n;
police_y = n;
}
else{
police_x = p[police-1].first;
police_y = p[police-1].second;
}
target_x = p[target-1].first;
target_y = p[target-1].second;
return abs(police_x-target_x) + abs(police_y-target_y);
}
int find_distance(int police1, int police2){
/*
두 경찰차가 현재 police1, police2 사건을 마지막으로 맡았을때
이후로 최소 비용 출력
ex) find_distance(3,5) 라고 하면
이제 6번째 사건을 처리할 차례이므로
첫번째 경찰차가 6번사건을 맡거나 = find_distance(6,5) + 3->6 거리
두번째 경찰차가 6번사건을 맡아야한다. = find_distance(3,6) + 5->6 거리
그리고 두 경찰차중 어느 경찰차가 움직여야하는 지를
police_store[police1][police2]에 저장한다.(1 or 2)
*/
// cout << police1 << " | " << police2 << endl;
if(police1 == w || police2 == w){
return 0;
}
int tmp1, tmp2, move;
move = max(police1, police2) + 1;
if(store[police1][police2] != -1){
return store[police1][police2];
}
if(police1 == 0){
tmp1 = find_distance(move,police2) + calculate_distance(police1, move, 1);
}
else{
tmp1 = find_distance(move,police2) + calculate_distance(police1, move, 0);
}
if(police2 == 0){
tmp2 = find_distance(police1,move) + calculate_distance(police2, move, 2);
}
else{
tmp2 = find_distance(police1,move) + calculate_distance(police2, move, 0);
}
store[police1][police2] = min(tmp1,tmp2);
if(tmp1 < tmp2){
police_store[police1][police2] = 1;
}
else{
police_store[police1][police2] = 2;
}
return min(tmp1,tmp2);
}
int main(){
int tmp1,tmp2;
cin >> n;
cin >> w;
for(int i=0;i<w;i++){
cin >> tmp1;
cin >> tmp2;
p.push_back(make_pair(tmp1,tmp2));
}
for(int i=0;i<1010;i++){
for(int j=0;j<1010;j++){
store[i][j] = -1;
police_store[i][j] = -1;
}
}
cout << find_distance(0,0) << endl;
int x = 0;
int y = 0;
for(int i=0;i<w;i++){
cout << police_store[x][y] << endl;
if(police_store[x][y] == 1){
x = i+1;
}
else{
y = i+1;
}
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| [알고리즘][15][백준_2533] - 사회망 서비스 (0) | 2021.03.04 |
|---|---|
| [알고리즘] [14][백준_11724] - 연결 요소의 개수 (0) | 2021.01.31 |
| [알고리즘][12][백준_7576][c++] - 토마토 (0) | 2021.01.23 |
| [알고리즘][11][백준_1029][C언어] - 그림교환 (0) | 2020.03.04 |
| [알고리즘][10][백준_1126][C언어] - 같은 탑 (0) | 2020.02.29 |




