| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 기술면접
- 백준11053
- 백준12738
- 2482
- 개발자 면접
- Python
- 정상회담2
- 카카오 서류전형
- 알고리즘
- LIS
- 카카오 면접
- 카카오 인턴십
- 카카오 인턴
- 가장긴증가하는 부분수열
- 카카오
- 2228
- 백준12015
- 여름인턴십
- 파이썬
- Longest Increasing Subsequence
- 1670
- 인턴십 면접
- 최장증가수열
- 카카오 자기소개서
- 백준
- 2629
- DP
- 단어수학
- 구간나누기
- LIS 알고리즘
- Today
- Total
프로그래밍에 대한 고찰 및 생각
[알고리즘][4][백준_2482][Python3] - 색상환 본문

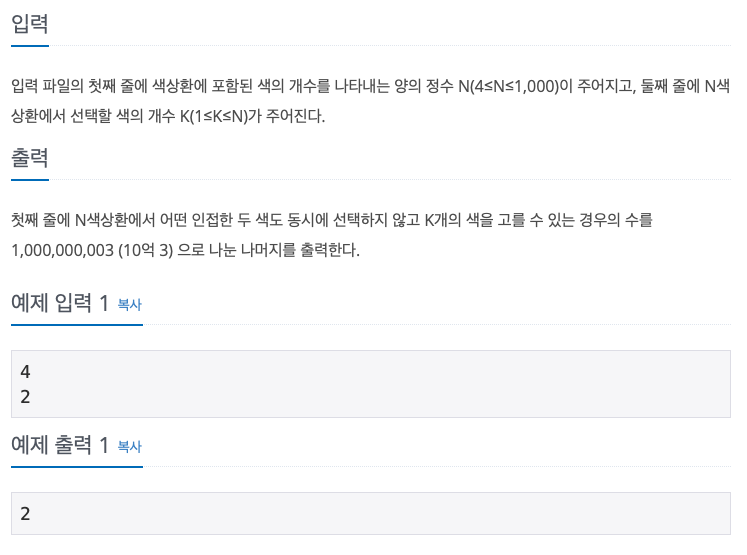
문제이해
문제에서는 다채로운 색이 등장하지만 단순하게 n등분 되어있는 원에서 인접하지않게 k개를 색칠하는 경우의 수를 구하는 문제이다.
알고리즘 전략
알고리즘 구현을 위한 첫걸음은 노트북에서 잠시 손을 내려놓고 펜과 종이로 직접 구해보는것이다.
무언가 규칙성이 있을것같았고 점화식이 있을것같았다.
N=6 K=2 일때의 경우로 생각해보자
6개의 칸이 있고 2칸을 이웃하지않게 색칠하는 경우의 수를 구하는 문제이다.
이를 편의상 앞으로 color(6,2) 라고 하자
color(6,2)를 구하기 전에 color(5,2) 를 한번보자
color(5,2)는 다음과 같이 5가지이다
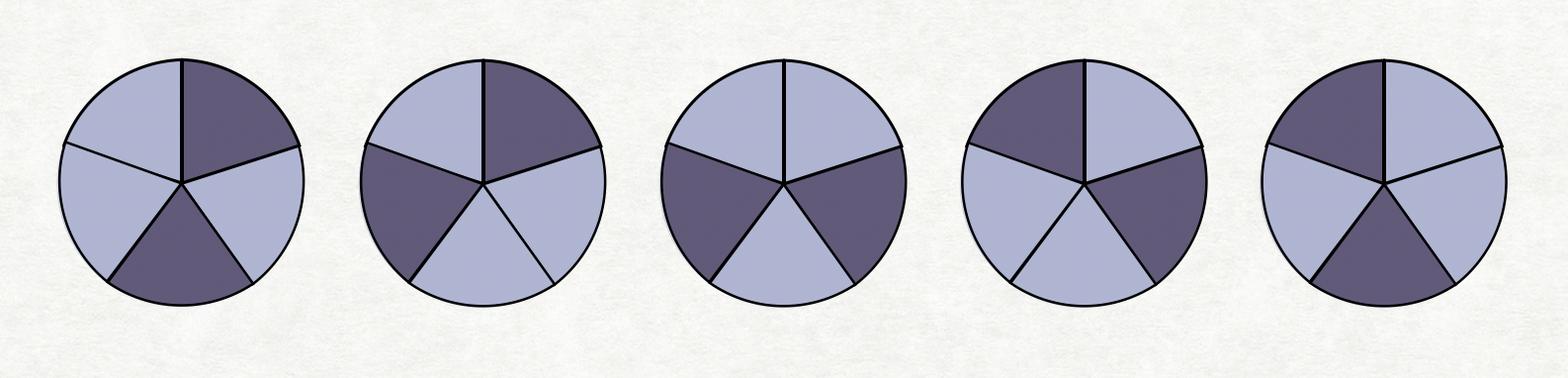
여기서 마지막 칸을 두개로 쪼갠다면 다음과 같다.
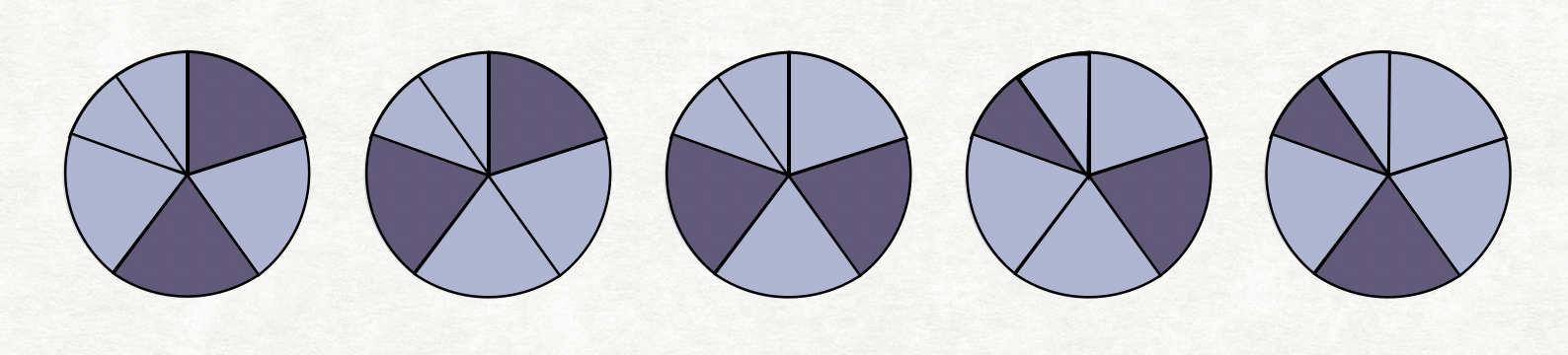
바로 위의 5가지 경우는 color(6,2) 의 경우의 수들중 일부이다.
color(6,2) = color(5,2) + A
이런식으로 점화식이 될것만 같은 느낌이온다.
그렇다면 나머지 A는 어떻게 접근해야할까?
한번 역으로 접근해보자.
color(6,2)의 모든 경우는 9가지로 다음과 같다.
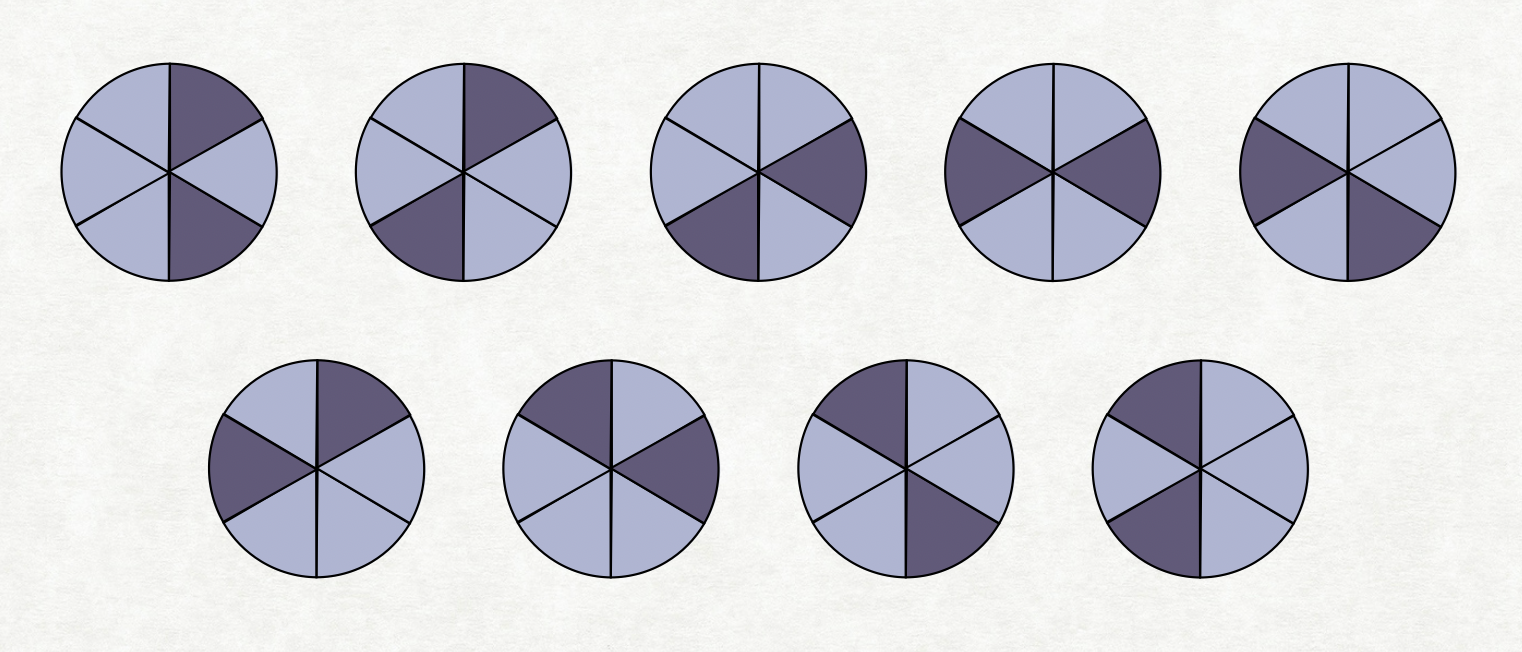
잘 살펴보면 위의 5가지가 color(5,2)와 같은 형태임을 알수 있다.
그렇다면 아래 4가지는 어떻게 도출해내는것일까?
먼저 전에 color(5,2)로부터 5개를 추출해왔을때로 돌아가보자 현재 5개까지는 6번째구역이 생기기전 5개의 구역만으로 만든 경우의수 이므로 마지막 6번째자리를 채운 경우의수가 빠져있다. 그경우가 바로 바로 위그림에서 아랫줄에서 오른쪽 3개이고 마지막으로 아랫줄 맨왼쪽 하나가 남아있다.
새로추가한 색을 무조건 하나 칠한다고 가정해보자
다음은 color(4,1)의 경우이다
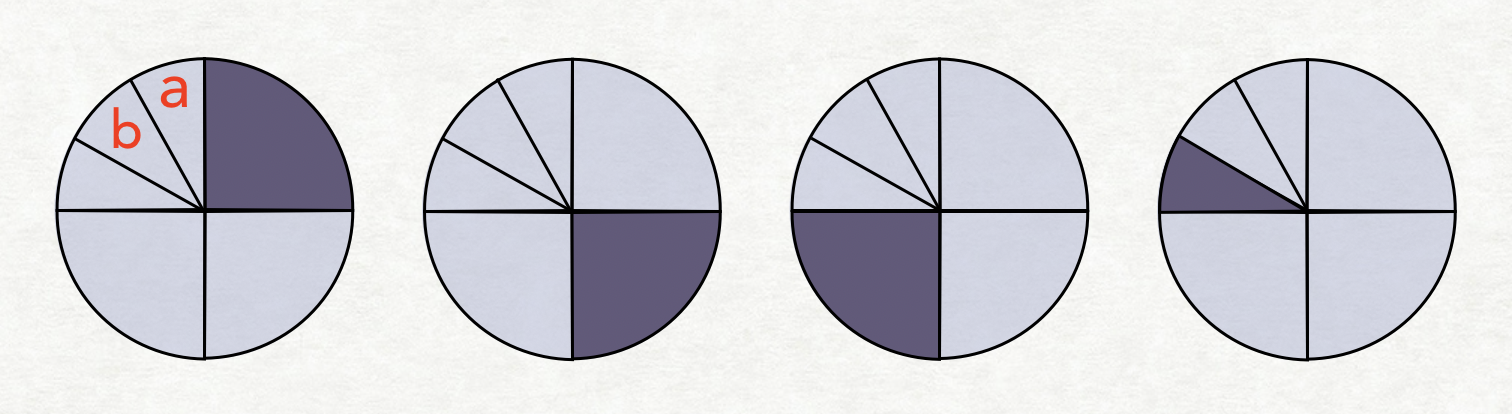
여기서 color(6,2)의 아랫줄 4개를 대입해보면 다음과같다
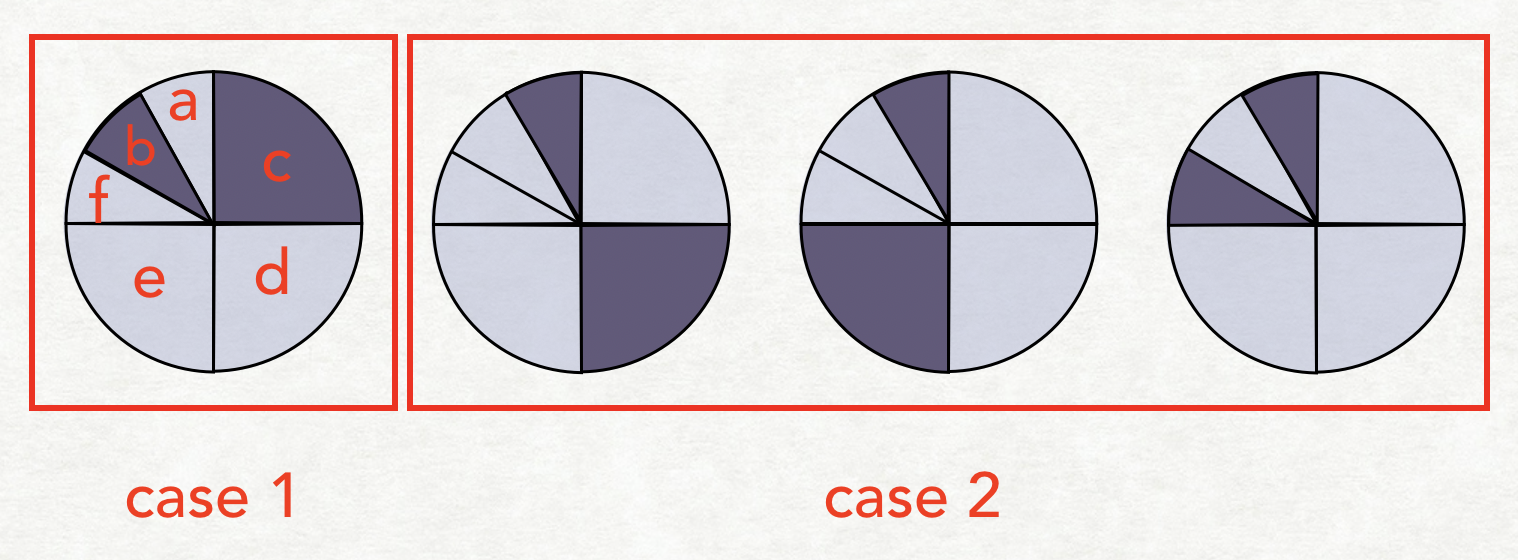
먼저 case 2의 경우 새로추가된 a(위 그림에서 빨간글씨 a) 를 반드시 칠한다는 조건하에 가능한 경우의 수이다.
여기까지는 좋다
그러나 case 1 에서 이런 의문점이 들어야한다.
A에서는 a를 무조건 칠하는 경우의 수라고 했는데 왜 case1 에서는 a가 색칠되어있지 않는지?
사실 정확히 말하자면
case 1에서 a에 색이 칠해졌어야 맞는것인데 그러면 그 오른쪽과 맞닿아 버리기 때문에 한칸 왼쪽으로 옮긴것이다.
이것이 왜 가능한가?
천천히 생각해보면 우리는 처음에 6칸짜리의 경우의 수를 고려하고 있고 현재는 4칸에서의 경우의 수를 보고있다.
사실 color(5,2)의 측면에서는 a 한칸이 추가된것이지만
color(4,1)의 입장에서는 a와 b 두칸이 추가된 것이다. 이얘기는 원래 color(4,1)의 경우에서 c 와 f는 본래 동시에 칠해질수 없는 구역이다.
따라서 c와 f 둘중 최대 한구역만 색칠되어있으므로 만약 c구역이 칠해져있는 경우면 b를, 그렇지 않다면 a를 칠할수 있는것이다.
여기서 한가지더 생각해볼 부분이 있다.
위의 그림에서 두번째상황일때(a,d 가 칠해져있을때) a말고 b를 칠할수도 있으니 c, f 두곳 모두 비어있다면 a,b모두 칠할수 있으므로 경우의수가 두개여서 color(4,1)보다 커져야 되는것 아닌가?
하지만 신기하게도 a를 못칠하는 경우가 아닌데 b대신 a를 칠해버리면 color(5,2)에서 구한 것과 중복이 발생한다.
그 이유는 case 1 에서 a대신 b를 칠해도 중복이 발생하지 않는 이유에 있다.
바로 color(5,2) 관점에서 봤을 때 a가 없다면 사실 b와 c는 붙어있는 구간이므로 둘다 색칠할수 없는 경우이다. 따라서 이는 어디에서도 중복되지않고 첫 경우이므로 옮길수 있는것이다.
지금까지 한 내용을 정리하면 정리하면 다음과 같다

따라서
color(n,k) = color(n-1,k) + color(n-2,k-1) 로 일반화 할수 있다.
표를 조금만 그려보면 알수 있듯이
k = 1일때는 항상 경우의수가 n을 따라가며
n/k = 2일때는 항상 두가지 경우만 존재한다
이를 이용해서 최종적으로 코드를 작성하면 다음과 같다.
import sys
sys.setrecursionlimit(10000000)
def color(n,k,answer):
if(n/k == 2):
return 2
if(k == 1):
return n
if(answer[n][k] == 0):
total = color(n-1,k,answer) + color(n-2,k-1,answer)
answer[n][k] = total
return total
else:
return answer[n][k]
n = int(input(""))
k = int(input(""))
answer = [[0]*(n+1) for i in range(n+1)]
if(n/2 < k):
print(0)
else:
print(color(n,k,answer)%1000000003)
사실 이문제는 몇가지 케이스를 직접 구해보고 점화식을 유추해서 풀수도 있지만 왜 그런 점화식이 나오게 되는지 본질을 공부하는것이 나중에 이보다 더 심화된 문제가 주어졌을때 그 연관성을 스스로 유추할수 있는 능력을 키워준다고 생각한다.
그런 관점에서 이 문제는 생각하는 힘을 길러주는데 아주 좋은 문제인것 같다.
'알고리즘 > 백준' 카테고리의 다른 글
| [알고리즘][6][백준_1670][Python3] - 정상 회담 2 (0) | 2020.02.06 |
|---|---|
| [알고리즘][5][백준_1103][Python3] - 게임 (0) | 2020.02.02 |
| [알고리즘][3][백준_2228][Python3] - 구간 나누기 (0) | 2020.01.15 |
| [알고리즘][2][백준_2629][Python3] - 양팔저울 (1) | 2020.01.14 |
| [알고리즘][1][백준_1339][Python3] - 단어 수학 (0) | 2020.01.14 |




