| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 1670
- 2228
- 구간나누기
- 백준
- 카카오 자기소개서
- 카카오 서류전형
- 기술면접
- 카카오 인턴십
- 카카오
- Python
- 단어수학
- 파이썬
- 백준12738
- Longest Increasing Subsequence
- 백준12015
- 2482
- 백준11053
- 정상회담2
- 알고리즘
- 2629
- 카카오 인턴
- 여름인턴십
- 최장증가수열
- LIS 알고리즘
- 가장긴증가하는 부분수열
- 인턴십 면접
- DP
- 개발자 면접
- 카카오 면접
- LIS
- Today
- Total
프로그래밍에 대한 고찰 및 생각
[알고리즘][5][백준_1103][Python3] - 게임 본문


문제이해
n x m 의 보드에 숫자들이 주어지고 특정지점에서 출발해서 특정조건에 따라 상하좌우로 이동하며 최대,최소의 경우를 구하는 전형적인 문제이다. 다만 여기서는 무한번 움직인다면 -1을 출력해야하므로 이부분이 까다로울수 있다.
알고리즘 전략
[0][0] 지점에서 시작해서 해당칸의 숫자만큼 상하좌우로 이동할수 있으므로 모든 경우를 확인해봐야한다.
따라서 재귀함수를 이용한 brute-force 와 메모이제이션을 이용해 DP로 해결하면 될것같다.
문제에따르면 최대한 보드 내에서 많이 움직여야하는데 보드바깥으로 나가거나 H를 만나면 종료되므로 해당조건으로 설계하면 이부분은 간단하다.
중요한 부분은 무한번 움직이는것을 어떻게 캐치해낼것인지이다.
쉽게생각하면 이런경우를 떠올릴수 있다.
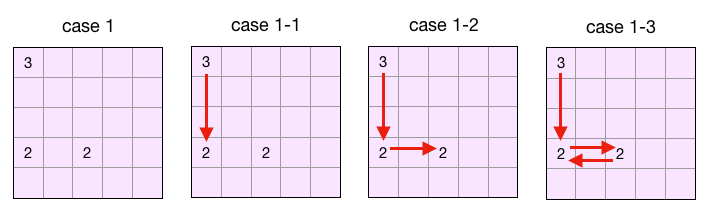
위 상황은 1-3을 보면 [3][0]과 [3][2] 에서 무한루프가 생기는것을 알수있다.
그렇다고 단순히 직전에있던 좌표와 현재좌표만 비교해서는 안된다.

이경우 [3][0]에서 [3][4] [1][4] [1][1] [3][1] 4칸을 거친후에 다시 [3][0]으로 돌아오게된다. 이또한 무한루프이다.
이런 무한루프를 캐치해낼수 있는 방법은 원소가 0인 n x m 의 2차원리스트(tmp라고하자) 를 만들고 어떤 칸에 접근할때 해당 i , j 인덱스가 0인지 1인지(기본이 0이므로 0이면 아직 방문을 안한상태, 1이면 방문을 한상태로 가정) 확인해서 0이라면 해당 칸의 인덱스를 1로 바꿔주고, 1이라면 이미 방문했는데 또 방문한것이므로 무한루프임을 알수있다.
그런데 m x n 칸에서 움직일수 있는 경로의 가지수가 매우 많은데 같은 칸을 방문했더라도 다른 경로라면 서로 충돌이 일어나서는 안된다.
따라서 재귀를 돌때 해당칸의 방문상태를 확인하고, 다시 미방문으로 처리해주는 순서가 매우 중요하다.
재귀에서는 return을 만나기전까지는 하나의 경로를 의미하므로 return을 만나기전까지는 tmp 배열의 값을 0으로 다시 초기화할필요가 없다. 하지만 return을 만난다면 무한루프임을 확인했거나 경로가 없어서 종료해야하는 상황이므로 return 하기전에 방문했던 해당 칸의 tmp를 0으로 다시 바꿔주어야한다.
import sys
sys.setrecursionlimit(10000000)
def dpp(check,maze,dp,i,j,n,m,bi,bj,first):
if(i < 0 or j < 0 or i > (n-1) or j > (m-1)):
return 0
if(maze[i][j] == 'H'):
return 0
if(check[i][j] == 0):
check[i][j] = 1
else:
return "inf"
maximum = 0
if(dp[i][j] != -1):
check[i][j] = 0
return dp[i][j]
tmp1 = dpp(check,maze,dp,i+maze[i][j],j,n,m,i,j,first)
tmp2 = dpp(check,maze,dp,i,j+maze[i][j],n,m,i,j,first)
tmp3 = dpp(check,maze,dp,i-maze[i][j],j,n,m,i,j,first)
tmp4 = dpp(check,maze,dp,i,j-maze[i][j],n,m,i,j,first)
if(tmp1 == "inf" or tmp2 == "inf" or tmp3 == "inf" or tmp4 == "inf"):
check[i][j] = 0
dp[i][j] = 'inf'
return "inf"
# "inf"는 무한루프가 생겼음을 의미하며 하나라도 inf가 있다면 어떤경로가 더 최대인지 상관없이 inf만
# 리턴하게되며 최종 리턴도 inf가 되어 마지막에 -1을 출력하게 된다.
maximum = max(tmp1,tmp2,tmp3,tmp4)+1
dp[i][j] = maximum
check[i][j] = 0
return maximum
n,m = input().split(" ")
n = int(n)
m = int(m)
maze = [[0]* (m+1) for i in range(n+1)]
check = [[0]* (m+1) for i in range(n+1)]
for i in range(n):
a = input()
for j in range(len(a)):
if(a[j] != "H"):
maze[i][j] = int(a[j])
else:
maze[i][j] = a[j]
dp = [[-1]* (m+1) for i in range(n+1)]
first = False
final = dpp(check,maze,dp,0,0,n,m,0,0,first)
if(final == "inf"):
print(-1)
else:
print(final)
'알고리즘 > 백준' 카테고리의 다른 글
| [알고리즘][7][백준_1648][Python3] - 격자판 채우기 (0) | 2020.02.06 |
|---|---|
| [알고리즘][6][백준_1670][Python3] - 정상 회담 2 (0) | 2020.02.06 |
| [알고리즘][4][백준_2482][Python3] - 색상환 (0) | 2020.01.15 |
| [알고리즘][3][백준_2228][Python3] - 구간 나누기 (0) | 2020.01.15 |
| [알고리즘][2][백준_2629][Python3] - 양팔저울 (1) | 2020.01.14 |




