| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Longest Increasing Subsequence
- 기술면접
- 정상회담2
- 단어수학
- 알고리즘
- 카카오 서류전형
- 최장증가수열
- 백준11053
- 가장긴증가하는 부분수열
- 카카오 자기소개서
- Python
- 파이썬
- 2482
- 카카오 인턴십
- 개발자 면접
- 2228
- LIS 알고리즘
- 백준12738
- 2629
- 1670
- 인턴십 면접
- 백준12015
- 여름인턴십
- 카카오
- LIS
- 구간나누기
- 카카오 면접
- 백준
- DP
- 카카오 인턴
- Today
- Total
프로그래밍에 대한 고찰 및 생각
[탐욕 알고리즘][1] - 개요 본문
탐욕 알고리즘(Greedy Algorithm)
탐욕 알고리즘(이하 그리디)은 어떤 문제를 해결할때 모든 경우의 수를 전부 고려하지 않고 항상 최적이 되는 것만 골라서 진행해나가는 알고리즘을 의미한다.
모든 경우의 수를 전부 고려해서 최적의 해를 계산해내는 dynamic programming과는 다르다.
그렇다면 두가지 의문이 들수있다.
1. 항상 최적의 해만 골라서 탐색하면 지금까지 왜 dynamic programming으로 모든 경우의 수를 분석했나?
왜냐하면 그리디 알고리즘으로 모든 문제를 해결할 수 있는것이 아니기때문이다.
현재 상황에서는 가장 최적의 해라고 생각했지만 이후에 상황에 따라 그때의 선택이 최선의 결과를 만들지 않을수도 있기때문이다.
2. 그렇다면 그리디 알고리즘은 최선일수도 있고 아닐수도 있는 찔러보기식 알고리즘인가?
다른 알고리즘으로 구현하였을때 시간복잡도가 굉장히 높게나올경우 그리디 알고리즘으로 대체하여 사용할수 있다.
(물론 그 해가 best 라고 장담할수는 없지만 그래도 나름 최적화가 되어서 실용적으로 사용할 정도는 될수있다.)
또한 정확한 증명만 뒷받침되어있다면 최적의 해를 도출해 낼수도 있다.
Greedy 적인 접근(1)
그렇다면 Greedy하게 접근한다는 것이 무엇일까
아래 문제를 통해 살펴보자.

이 문제는 아래와 같이 숫자와 + - 기호들로 이루어진 식이 주어졌을때 괄호를 자유롭게 사용해서 최종 결과가 최소가 되게 만드는 문제이다.
일반적인 dp 방법으로 해결하려 한다면 괄호를 사용할수 있는 모든 경우의 수를 계산해서 그중 가장 최소가 되는 답을 골라낼것이다.
그러나 Greedy한 접근에서는 모든 경우의 수를 고려하지 않고 각 상황마다 최적의 해를 도출하기 위한 액션을 취한다.
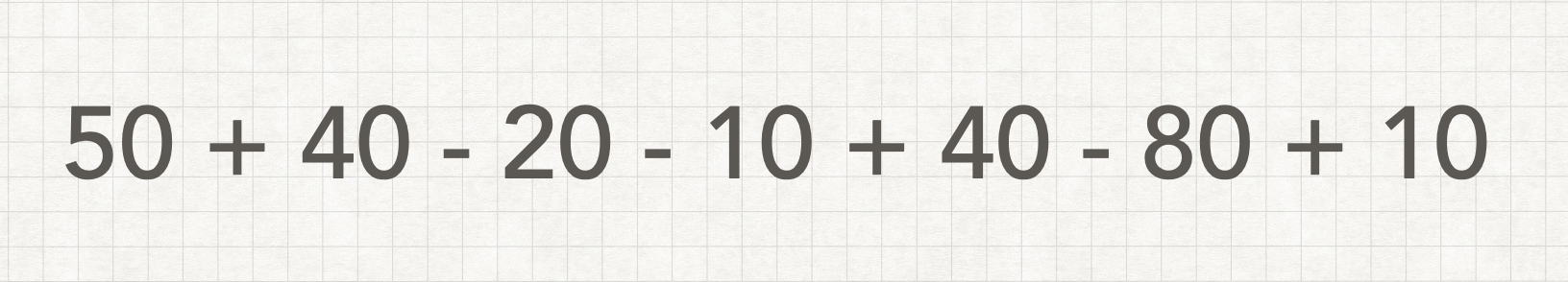
그러기 위해서는 먼저 문제에서 주어진 목적에 대해 잘 살펴봐야한다.
이 알고리즘의 최종 목표는 이 식의 값을 최소로 만드는 것이다.
그리고 주어진 조건들의 성질에 대해서도 잘 살펴봐야한다.
괄호의 경우 - 바로 뒤에 붙이면 그 이후 양수들을 모두 음수로 바꿀수있다.
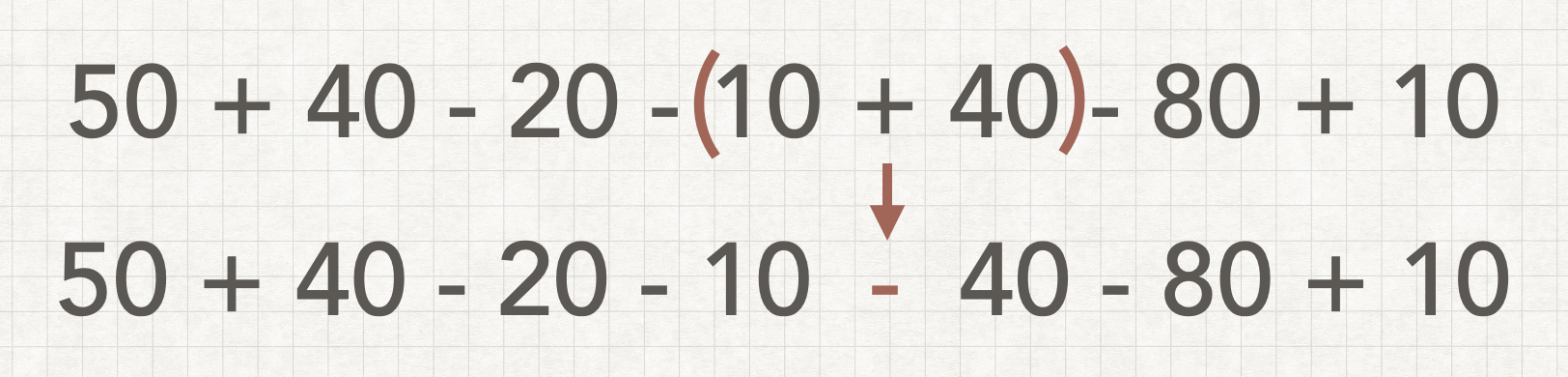
위의 식에서 -10 에 괄호를 쳐서 40까지 묶으면 원래는 +40으로 계산될값이 -40으로 계산되어 더 최소값을 만들게된다.
바로 이 성질을 이용하여 일련의 조건들을 정하는 것이다.
condition. 음수 기호가 나올경우 해당 숫자부터 다음 음수기호가 나오기전 or 식의 끝까지 묶어준다.
위의 조건을 사용하게 되면 기존에 +로 계산될 값들이 -로 치환되어 최종적으로 값을 작게 만드므로 뭔가 야매? 스러운 방법처럼 되었다.
그렇다면 마지막으로 이러한 접근이 진짜 모든 경우에 있어서 항상 최적의 해를 만드는 조건인지 생각해보자.
문제에서는 양수기호와 음수기호가 주어진다. 최종 값을 만드려면 음수 기호들은 살리고 최대한 양수기호들을 음수기호로 바꾸어야한다.
음수 기호뒤에 나오는 모든 양수 기호들은 위의 조건에 의해 음수 기호로 바꿀수있다.
하지만 양수기호 이전에 음수기호가 없다면 아무리 괄호를 쳐도 그 기호를 음수로 바꿀수 없다.
즉 문제에서 우리에게 권한을 준것은 오로지 괄호를 치는것뿐이고 우리가 여기서 할수있는 것은 음수기호뒤에 있는 양수기호들을 모두 음수기호로 바꿔주는것이다.
따라서 이 방법이 항상 최적의 해(가장 최소가 되는값)를 만들어 줄것이라고 확신할수 있다.
Greedy 적인 접근(2)

다른 문제를 보자.
이 문제의 경우 알고리즘의 최종 목적은 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값이다.
이런 문제의 경우 매우 극단적인 예시를 통해 그리디한 접근을 찾는것이 방법이 될수있다.
만약 5명이 사람이 있고 각각 인출하는데 필요한 시간이 1000분, 1분, 1분, 1분, 1분 이라고 하자.
그렇다면 인출하는데 1분이 걸리는 사람들이 먼저하고 마지막에 1000분이 걸리는 사람이 하는것이 시간의 합이 최소가 될지,
아니면 1000분이 걸리는 사람이 먼저 인출하고 나머지 1분이 걸리는 사람들이 인출을 할지
고민을 해보면 답이 나올것이다.
너무나 당연하게도 1분이 걸리는 사람들이 먼저 인출을 빠르게 마치고 마지막에 1000분이 걸리는 사람이 인출을 하는것이 시간의 합이 최소가 될것이다.
여기서 알수있는 접근법은 사람들의 인출시간을 오름차순으로 정렬한뒤 맨 앞부터 sum값을 sum하는것이다.
인출시간이 짧은 사람이 먼저 인출하는것에 대한 수학적인 증명도 간단히 할수있다.

위의 수식에 따르면 1번이 먼저 인출할때가 2번이 먼저 인출할때보다 k분을 절약할수있다.
'알고리즘 > 탐욕 알고리즘 (Greedy)' 카테고리의 다른 글
| [탐욕 알고리즘][2] - 회의실 배정 문제 (4) | 2021.03.17 |
|---|

