| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 백준11053
- 개발자 면접
- 기술면접
- 카카오 인턴
- 2482
- 2629
- Longest Increasing Subsequence
- 파이썬
- 구간나누기
- 카카오 면접
- 2228
- Python
- 카카오 자기소개서
- 카카오 서류전형
- 카카오 인턴십
- LIS 알고리즘
- 백준12015
- 백준
- 1670
- 카카오
- LIS
- 알고리즘
- 인턴십 면접
- 가장긴증가하는 부분수열
- 단어수학
- 정상회담2
- 여름인턴십
- DP
- 백준12738
- 최장증가수열
- Today
- Total
프로그래밍에 대한 고찰 및 생각
[탐욕 알고리즘][2] - 회의실 배정 문제 본문
유명한 Greedy 알고리즘 - 회의실 배정 문제
회의실 배정 문제는 그리디 알고리즘에서 빠지지 않고 등장하는 문제이다.
이문제는 각 회의마다 시작시간과 종료시간이 정해져있고 하나의 회의실에 대해 가장 많은 회의를 진행하게 하고 싶을때 그 개수를 구하는 문제이다.
이 문제에서의 최종 목표는 최대한 많은 회의를 진행시키는 것 이다.
여기서 조건은 회의마다 시작시간과 끝나는시간이 정해져있다는 것과, 두 회의간 겹쳐서는 안된다는 점이다.
Think1. 가장 짧은 회의들 먼저 진행시키면 되지않을까?
굉장히 Greedy한 접근법이다.
최대한 많은 회의를 진행시키려면 결국 회의시간이 짧은 회의들을 골라서 넣는것이 최적의 해를 만들어 줄것같다.
과연 그럴까?

위와같이 a~g까지 7개의 회의들이 있다고 가정해보자.
여기서 위의 방법대로라면 아래와같이 회의시간이 가장 짧은 순서대로 골라서 g -> a -> d 순으로 회의를 골라서 진행할 것이다.

그러면 총 3개의 회의를 진행할수 있게된다.
하지만 아래와같이 선택하면 4개의 회의를 진행할 수 있다.

따라서 이 방법은 항상 최적의 해를 구해줄수 없다.
Think2. 가장빨리 끝나는 회의부터 넣으면 어떨까?
이것 또한 굉장히 Greedy한 접근이다. 위의 예시를 이방법으로 접근해본다면
가장 빨리 끝나는 회의가 a이므로 a 회의를 선택한다.


이후 빨리끝나는 회의는 b지만 a와 겹치므로 다음으로 빨리끝나는 회의인 c,d중 하나를 고르는데 끝나는 시간이 같을경우 더 늦게시작하는 회의를 고르도록 하자 (이 이유는 뒤에서 다루도록하자)

그리고 다음으로 빨리끝나는 회의인 f를 선택하고 마지막으로 g 회의를 선택하게 된다.


총 4개의 회의를 진행할수 있게되었고 주어진 상황에 있어서 최적의 해이다.
Proof. 해당 접근법에 대한 증명
과연 이 해가 도출된 것이 우연일까 아니면 항상 최적의 해를 도출해낼까?
만약 아래와같이 전체 회의 시간이 있고 가장 빨리 끝나는 회의가 k에 끝나는 회의라고 하자.
이 회의를 진행하게 되면 앞으로 우리는 하늘색 영역에 있는 시간들만 이용할수 있게된다.

그런데 만약 k보다 늦게 끝나는 회의를 먼저 잡으면 어떻게 될까?
아래와 같이 k'에 끝나는 회의를 선택하게 되면 회의에 사용할수 있는 시간이 적어진다.
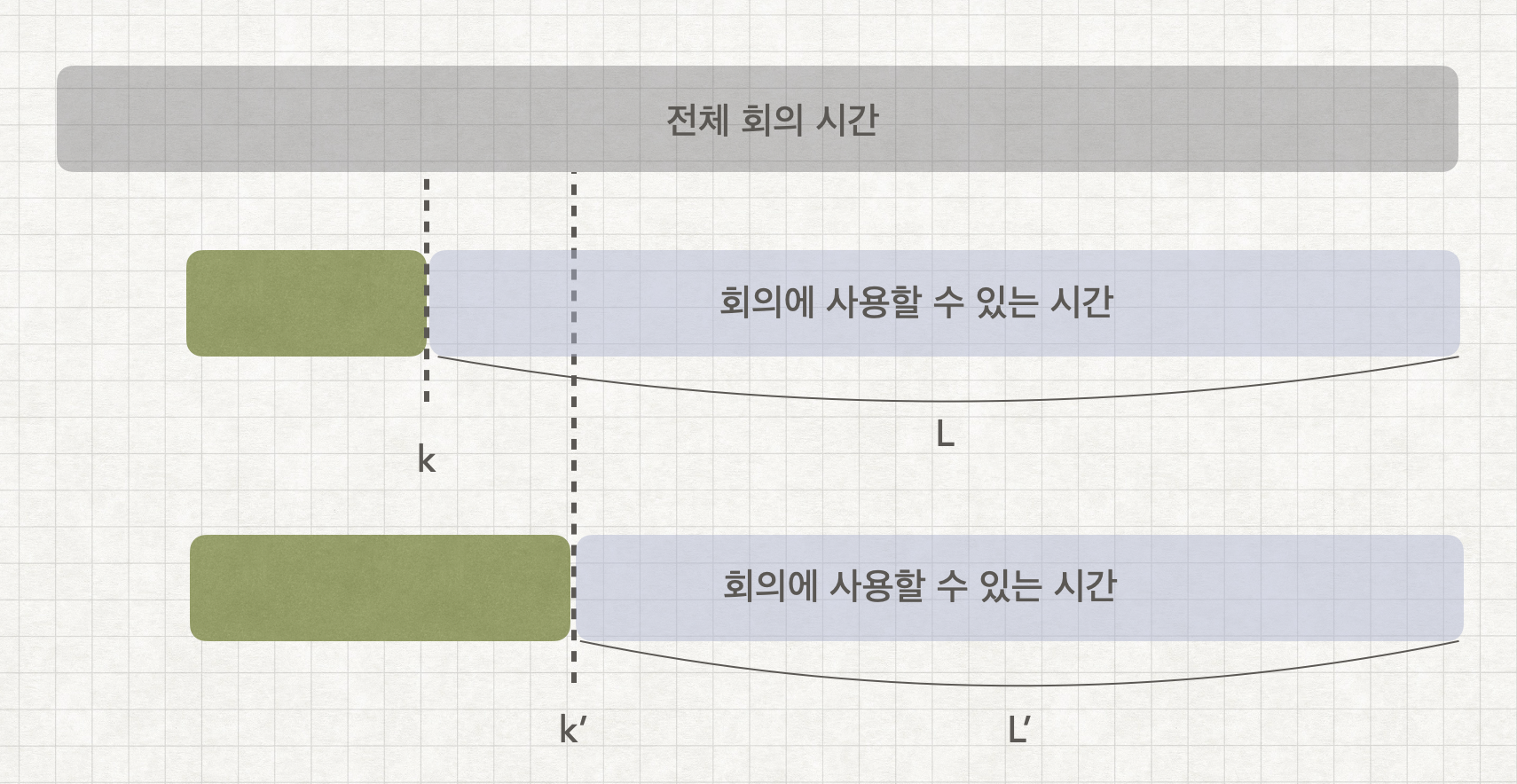
k에 끝나는 회의를 고르는것이 k'에 끝나는 회의를 고르는것보다 최적의 방법이라는 것을 반박하기 위해서는 L이라는 남은 시간보다 L'라는 남은시간에 회의들을 배치하는것이 더 많은 회의를 넣을 수 있다는 것을 증명해야한다.
과연 같은 회의목록들을 가지고 더 적은 타임에 많은 회의들을 넣는것이 가능할까?
당연히 불가능 하다.
따라서 항상 가장 빨리 끝나는 회의를 선택하는것이 최적의 해를 도출해낸다고 볼수 있다.
구현.
이를 구현하기 위해서는 먼저 빨리 끝나는 회의들을 구하기 위해 우선순위 큐(priority queue) 를 이용하였다.
또한 위에서 끝나는 시간이 같을 경우 시작시간이 짧은것부터 회의에 넣는다고 했는데 그 이유는 문제에서 "회의의 시작시간과 끝나는 시간이 같을 수도 있다" 라는 조건 때문이다.
만약 5-10 까지 진행되는 회의와 10-10까지 진행되는 회의가 있다면
- 10-10 회의를 먼저 진행하면 5-10 회의를 진행할수 없지만
- 5-10 회의를 먼저 진행하면 10-10 회의를 진행할수 있기때문이다.
따라서 아래와 같이 구현할수 있다.
구현언어 : C++
#include <iostream>
#include <queue>
#include <utility>
using namespace std;
int n;
struct Sub{
int start;
int end;
};
struct cmp{
bool operator()(Sub a, Sub b){
if(a.end == b.end){ // 종료시간이 같을 경우 시작시간이 작은것부터
return a.start > b.start;
}
return a.end > b.end; // 종료시간이 빠른것부터
}
};
priority_queue<Sub, vector<Sub>, cmp> pq;
int main(){
int tmp1,tmp2;
cin >> n;
Sub sub;
for(int i=0;i<n;i++){
cin >> tmp1 >> tmp2;
sub.start = tmp1;
sub.end = tmp2;
pq.push(sub);
}
int end = 0;
int tot = 0;
while(pq.size() > 0){
sub = pq.top();
if(end <= sub.start){ // 현재 꺼낸 회의가 현재 가장 최근에 종료된 회의 이후일때
tot++;
end = sub.end;
}
pq.pop();
}
cout << tot;
}'알고리즘 > 탐욕 알고리즘 (Greedy)' 카테고리의 다른 글
| [탐욕 알고리즘][1] - 개요 (0) | 2021.03.17 |
|---|

